Intro

在ML中评估是一个很重要的环节，一般有以下集中评估方式：

• Accuracy(准确率）
• Precision(精确率）
• Recall(召回率）
• F1

这里主要说一下precision与recall。

在很多情况下，只用Accuracy来评估模型是不准确，并且不合乎常理的，比如一下三种情况：

• 偏斜类：1000人中有三个犯人，我们只需要将所有人设为无罪，准确率就可以达到99.7%
• 当预测正确的代价很高时：预测杀人法，并处以死刑，此时我们不希望错误预测任何一个人，并倾向于将所有人设为无罪，准确率会变得很低。
• 当预测错误的代价很高时：预测癌症发病率，这是我们会倾向于将所有可能发病的样本都标准为发病，准确率会变得很高，但是被误判的病人也非常多。

因此，我们要引入其他的评估方法。

混淆矩阵

T            Predicted
R            相关  不相关
U     检索到    A    B
E     未检索到   C    D

其中有四个变量：

• A：预测相关，被检索到(TP)
• B：预测不相关，被检索到（FP)
• C：预测相关，未被检索到（FN)
• D：预测不相关，未被检索到（TN）

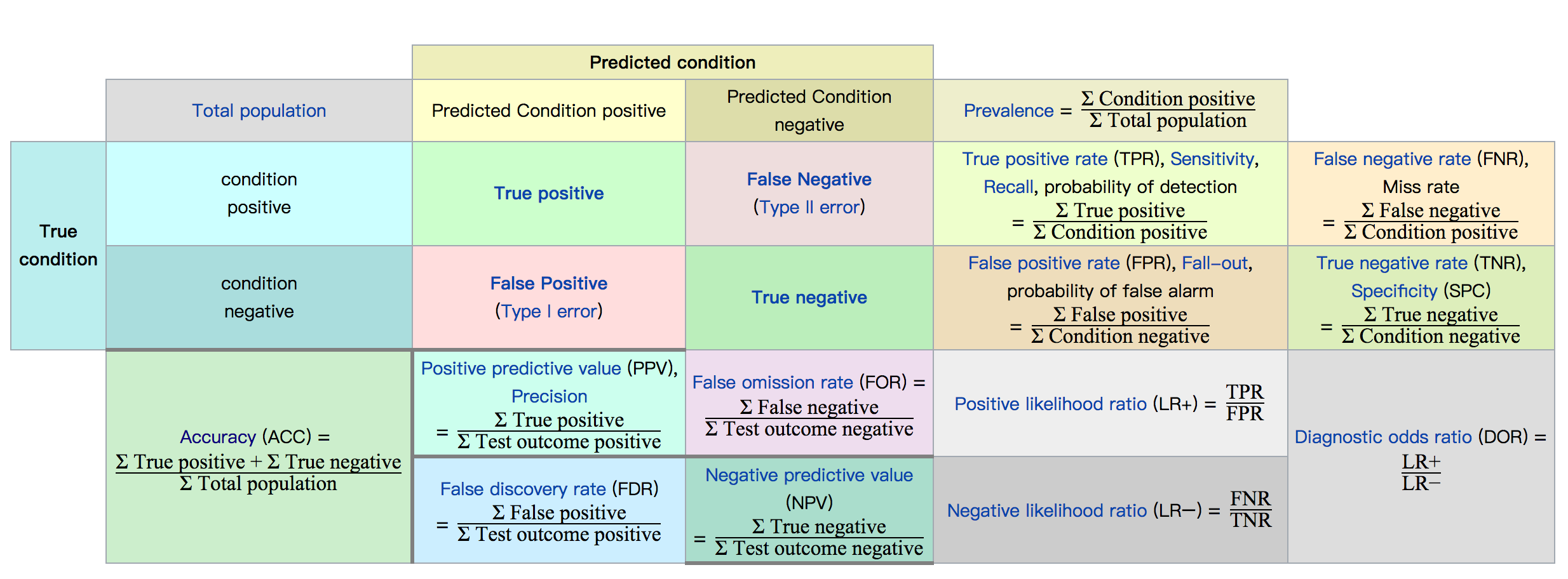
可以通过这个矩阵得到各种评估方式的计算方法：

TP: 本该为正例，被预测为正例。
TN: 被该为负例，被预测为负例。
FP: 本该为正例，被预测为负例。
FN: 本该为负例，被预测为正例。

• Accuracy = (TP + TN) / (P + N)
• Precision = TP / (TP + FP)
• Recall = TP / (TP + FN)

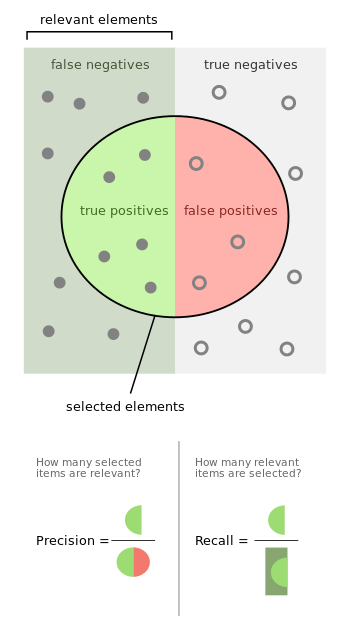
从计算方式我们可以大体确认这几个评估指标的意义：

Precision（精确度）: 所有正确预测的正例，占所有正例的比率。
Recall(召回率）：所有正确预测的正例，占所有被预测为正例的比率。

F1 分数

既然我们已讨论了精确率和召回率，接下来可能要考虑的另一个指标是 F1 分数。F1 分数会同时考虑精确率和召回率，以便计算新的分数。

可将 F1 分数理解为精确率和召回率的加权平均值，其中 F1 分数的最佳值为 1、最差值为 0：

F1 = 2 (精确率 召回率) / (精确率 + 召回率)

回归指标

正如前面对问题的回归类型所做的介绍，我们处理的是根据连续数据进行预测的模型。在这里，我们更关注预测的接近程度。

例如，对于身高和体重预测，我们不是很关心模型能否将某人的体重 100% 准确地预测到小于零点几磅，但可能很关心模型如何能始终进行接近的预测（可能与个人的真实体重相差 3-4 磅）。

平均绝对误差

在统计学中可以使用绝对误差来测量误差，以找出预测值与真实值之间的差距。平均绝对误差的计算方法是，将各个样本的绝对误差汇总，然后根据数据点数量求出平均误差。通过将模型的所有绝对值加起来，可以避免因预测值比真实值过高或过低而抵销误差，并能获得用于评估模型的整体误差指标。

均方误差

均方误差是另一个经常用于测量模型性能的指标。与绝对误差相比，残差（预测值与真实值的差值）被求平方。

对残差求平方的一些好处是，自动将所有误差转换为正数、注重较大的误差而不是较小的误差以及在微积分中是可微的（可让我们找到最小值和最大值）。

回归分数函数

除了误差指标之外，scikit-learn还包括了两个分数指标，范围通常从0到1，值0为坏，而值1为最好的表现。

其中之一是R2分数，用来计算真值预测的可决系数。在 scikit-learn 里，这也是回归学习器默认的分数方法。

另一个是可释方差分数。